| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 |
- 마이크로소프트 ai school 6기
- 마이크로소프트 AI
- MS
- microsoft
- microsoft ai school 6기
- 마이크로소프트 ai 스쿨 6기
- msai
- microsoft ai school
- 마이크로소프트
- 마이크로소프트 ai 스클
- microsoft ai
- micsrosoft ai
- 마이크로소프트 ai 스쿨
- Today
- Total
연랩
[Microsoft AI School 6기] 2/4(30일차) 정리 - 딥러닝(Deep Learning), 신경망, 경사하강법 본문
[Microsoft AI School 6기] 2/4(30일차) 정리 - 딥러닝(Deep Learning), 신경망, 경사하강법
parkjiyon7 2025. 2. 4. 17:48파이썬으로 배우는 딥러닝(Deep Learning)
신경망
손글씨 숫자인식
Flatten: 신경망에서 입력으로 쓰기 위함

Flatten된 자료가 신경망에서 input으로 입력이 됨
숫자 인식의 경우 출력 노드는 10개(0~9)
즉,
input layer(28*28개의 숫자) -> Hidden Layer -> 출력 Layer(0~9)
이때, 출력 노드는 확률로 나옴(0일 확률이 0.01 ... 7일 확률이 0.9면 7로 판단)

용어 정리
- scalar [1]
- vector [1, 2]
- matrix [[1, 2], [3, 4]]
- tensor - 3차원 이상
이미지와 텐서
- 흑백 이미지: 행렬
- 흑백 이미지들의 데이터: 3차원 텐서
- 칼라 이미지: 3차원 텐서
- 칼라 이미지들의 데이터: 4차원 텐서
sample_weight.pkl

- 편향 벡터의 개수는 hidden layer node 수와 동일
- layer(층) 에서 node(뉴런) 수를 정하는 방법은 경험적
- 이렇게 weight 값을 계산하여 sample_weight.pkl 파일에 저장
이러한 손글씨 숫자 예측을 실습하여 보면 다음과 같다
실습
라이브러리 import

신경망 계산

먼저 위의 코드를 통해 mnist 데이터를 다운로드 하여 준다

위에서와 같이 계산한 신경망 weight 값을 불러온다.

weight를 이용하여 중간 결과 값 -> 활성화 함수를 각 단계마다 한 후.
최종값 Y를 구하여 준다


최종적으로 신경망 값을 적용하여 정확도 결과를 보면 위와 같다
잘못 예측한 결과 출력
잘못 예측한 결과를 출력하여 보려면 아래와 같이 코드를 작성할 수 있다

어떤 숫자를 잘못 예측하였는 지도 알 수 있는데, 이를 이미지로 출력하여 보면 다음과 같다

잘못된 결과에는 육안으로 보기에도 헷갈리는 숫자도 있지만, 누가 봐도 잘못 예측된 결과도 있다

배치(묶음 처리)
- 숫자 데이터를 개별로 처리하면 I/O에서 병목현상이 발생함
- 입력 데이터 묶음 처리를 통해 I/O에 주는 부하를 줄임
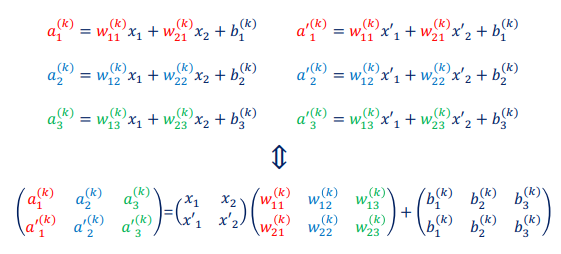
실습 - MNIST 데이터 배치로 숫자인식
묶음(batch) 단위로 predict에 입력, 출력도 batch 단위로
-> 낭비되는 I/O를 줄일 수 있음
라이브러리 import

신경망 계산
앞선 계산과 마찬가지로 신경망을 계산하여 준다

신경망 계산 -Batch

계산 시, batch 단위로 계산하게끔 구성한다
x_batch는 100개 단위로 구성하여 입력한다
y_ batch는 이에 대한 예측값을 100개 단위로 저장한다

이 중 가장 확률이 높은 값을 p에 저장 한다
batch_size =100이므로 p는 100개

label(t[i])에 있는 값 중 p와 같은 것이 있으면 그것만큼 합하여 accuracy_cnt를 증가하여 정확도를 계산한다.
이에 대한 결과는 다음과 같다

즉, t[i:i_batch_size] 하여 p와 같은 갯수 만큼 sum하여 accuracy_cnt에 추가하여 정확도를 계산한다.
-> 아까 보다 속도가 빨리 계산됨을 알 수 있다
신경망 학습
손실 학습
Rule-based vs. Data-driven
Rule-based 학습 : 명시적인 규칙을 사용하여 데이터를 분류하거나 예측하는 접근법
Data-driven 학습 : 대량의 데이터에서 패턴을 학습하고 예측 모델을 생성하는 접근법
-> 신경망(딥러닝)은 주로 Data-Driven 사용
손실함수(Loss function)
- 모델의 예측값과 실제값 간의 차이를 측정하는 함수
- 모델의 성능을 평가하고 모델의 가중치를 업데이트하여 학습을 진행하는데 중요한 역할을 함.
- 손실함수의 출력은 주어진 데이터셋에 대한 모델의 예측 정확도를 수치적으로 나타남
손실 함수의 종류
- 평균 제곱 오차(Mean Square Error)
- 교차 엔트로피 오차(Cross Entropy Error)
예시)
숫자 이미지가 2 인 두 개의 이미지의 Softmax 값을 구한 두가지 경우

y(확률-예측)과 정답(t)의 차이의 제곱을 계산
-> 손실 함수의 값이 작으면 성능이 높다고 평가
교차 엔트로피 오차(Cross Entropy Error)
- 교차 엔트로피는 정보이론에서 확률분포사이의 거리를 재는 방법
- 데이터가 신경망을 거쳐 나온 확률 벡터와 라벨로 구한 교차 엔트로피
- 정답에 해당하는 출력이 커질수록 0에 다가가다가 그 출력이 1일때 0이 된다
- 반대로 정답일 때의 출력이 작아질수록 오차는 커진다
손실함수를 설정하는 이유
- 신경망 학습에서는 최적의 매개변수(가중치와 편향)을 탐색할때 손실함수의 값을 가능한 한 작게하는 매개변수 값을 찾음.
- 이때 매개변수의 미분(정확히는 기울기)을 계산하고, 그 미분 값을 단서로 매개변수의 값을 서서히 갱신하는 과정을 반복함
- 손실함수에서 기울기가 작은 쪽으로 weight와 편향을 이동하는 과정을 학습이라고 함
-> 결과값과 정답과의 차이를 나타내주는 손실 함수 -> 이를 통해 weight와 bias를 업데이트
- 손실 함수는 마지막 predict와 정답값을 비교하여 역으로 일괄 조정
수치 미분
손실 함수의 기울기가 0인 지점이 최소 -> 미분을 통해 구하기
수치 미분
함수의 미분값을 해석적(수학적 공식)으로 구하지 않고 컴퓨터를 이용해 수치적으로 근사하는 방법

h의 값을 10^(-4) 으로 설정하여 해석적 방법과 최대한 근사한 미분값을 구함
- lim -> 0이라는 개념을 컴퓨터로 표현할 수 없으므로 작은 수 h를 대입
-> 컴퓨터는 미분을 하는 정확한 미분공식이 있는 것이 아니라 작은 값 h를 사용
이를 코드로 나타내어 계산 하면 다음과 같다

미분할 함수를 function_1로 하고 이를 f로 하여 numerical_diff에 넘겨주면 미분 공식에 대입하여 기울기를 구할 수 있다.
이렇게 구한 기울기를 tangent_line에 대입하면 접선의 공식을 구할 수 있다(lambda를 통해 함수를 리턴값으로 넘겨줌)
이렇게 하여 함수와 그 접선을 그려준 결과는 다음과 같다

5에서의 접선을 구한 결과는 위와 같다.
기울기가 0.199 즉, 2임을 알 수 있다.
기울기
일변수 미분 vs 다변수 미분(편미분)
한 개의 변수에 대해 미분하는 것을 일변수 미분

아래 함수와 같이 변수가 2개(점)일때 각 축에 대해 미분하는 것을 편미분

위의 사진에서의 3차원 평면의 기울기를 화살표로 표현 해보면 다음과 같다

여기에서 미분 한 부분을 살펴 보면,


즉, 각 변수에 대하여 편미분을 하는 부분인 것을 알 수 있다
또한,

- X가 1차원 배열이면, 그냥 _numerical_gradient_no_batch를 호출해서 편미분을 계산
- X가 2차원 배열이면, 각 행마다 편미분을 수행해서 grad 배열을 채움
이를 그림으로 그려 보면 다음과 같다


위의 그림은 아래와 같이 생긴 평면에서 기울기를 계산한 결과이다. 기울기가 최소가 되는 지점으로 화살표가 가리키고 있으며, 최소가 되는 지점과의 거리가 화살표의 길이이다.
DNN 학습: 순전파와 역전파
- Forward Propagation : Input à Output 방향으로 출력값을 계산하는 과정. 실측값과 차이인 오차(loss) 계산
- Back Propagation : Output à Input 방향으로 가중치를 갱신하는 과정. 딥 러닝에서 학습이 이루어짐


경사하강법(Gradient Descent)
- 역전파는 출력값과 실제값의 차이인 오차가 최소가 되도록 가중치를 갱신함
- 이때 가중치 갱신 방법으로 경사 하강법을 사용함

기울기가 -면 더해주고 +면 빼주는 형태로 진행
- 오차가 낮아지는 방향으로 이동할 목적으로 미분
- 가중치 업데이트 : 미분값을 가중치에서 빼 줌으로써 w 값을 줄임

n: 에타
기울기 값을 다 반영하는 것이 아니라 일부 반영을 하여 기울기 값의 보폭을 조절함
-> learning rate 반영률을 조절
-> w+
이를 코드로 나타내면 다음과 같다

위의 코드에서 추가한 부분은 다음과 같다

여기에서 lr은 learning rate 즉, 얼마나 기울기를 반영할까(보폭)이며,
step_num은 보폭의 갯수이다
디폴트 값은 lr=0.01, step_num=100으로 하였다

이를 반영하면 위와 같은데,
계산된 기울기의 반영률인 lr만큼 step_num인 20번 이동한 것이다. 이에 대한 결과는 다음과 같다

여기에서 계산한 기울기를 반영하면 아래와 같이 나타난다
numerical_gradient 함수를 통해 얼마나 이동해야하는 지를 알 수 있다
step 한번은 역전파 한번, 순전파 한번이라고 생각할 수 있다

lr의 값을 너무 크게 설정하면 기울기가 튀게 되는데, 그러면 아래와 같이 나올 수 있다

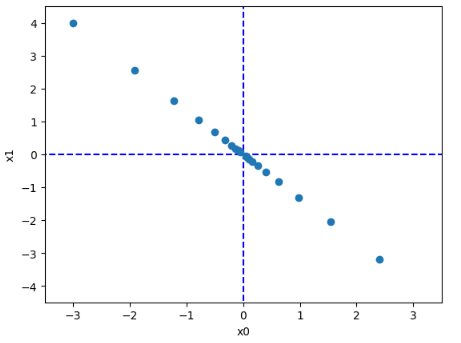
또한 step의 수가 모자라면 최소인 지점까지 도달하지 못할 수 있다.

- 현재 위치 xt에서 기울기 ∇f(xt)를 구한다.
- 기울기의 반대 방향으로 이동한다.
- 이 과정을 반복하여 최솟값에 점점 가까워진다

즉, 어떠한 점에서 기울기를 구하여 그 기울기의 일정 비율(lr) 만큼 반대 방향으로 이동
-> 최소인 지점을 찾을 수 있음
실습 - 정규분포로 초기화된 가중치(2x3)에 Cross entropy error 손실함수를 써서 새로운 가중치를 산출
1) 간단한 신경망을 만듦
2) weight 값은 랜덤으로 채움
3) 초기값 0.6과 0.9를 넣어서 손실 값을 만듦
-> 손실값에 해당하는 위치에서 기울기를 구함
-> 이 기울기를 구하여 weight에 반영할 예정
- simpleNet은 2 입력, 3 출력의 간단한 신경망입니다.
- 가중치 W를 사용해 입력 x를 변환하고, 소프트맥스로 확률을 구한 뒤, 손실을 계산
- numerical_gradient(f, W)를 통해 손실 함수의 기울기를 구함
- 이 기울기를 이용하면 경사 하강법(Gradient Descent)으로 최적의 를 찾아갈 수 있다
이를 코드로 작성하여 보면 다음과 같다

랜덤으로 가중치를 먼저 생성(randn(2, 3))하여 이를 예측함수에 넣음
-> y 값 구함
t는 정답 -> 이를 통해서 손실 값 계산
-> 손실 값의 기울기를 구함
학습 알고리즘 구현하기

배치(Batch)
데이터 세트 내의 데이터들을 한 개씩 학습 -> 컴퓨터 I/O의 제약, 불안정한 학습
-> 데이터 세트를 작은 덩어리(mini batch)로 나누어 처리하는 것이 효율적임
반복(Iteration)
- 에폭을 나누어 실행하는 횟수 = Mini batch의 갯수
에폭(Epoch)
전체 데이터 세트의 순전파/역전파를 한번 완료한 횟수를 의미
여러 번 수행해야 경사하강법의 효과를 볼 수 있음
- 에폭이 크면 : overfitting 문제
- 에폭이 작으면 : underfitting 문제

- 수정을 1회 마친 것으로 생각
미니배치 학습 : Stochastic Gradient Descent
- 훈련 데이터 중 무작위로 선별한 데이터를 미니 배치라고 함.
- 효율적인 계산, 수렴 속도 개선, 학습속도 개선
오늘의 간단한 후기
실습을 통해 이해를 할 수 있어 이해의 정도가 증가한 것 같다. 사실 편미분 너우 오래 전에 배워서 기억이 잘 안났다. 수학이 상당 부분 딥러닝에서 차지하고 있다는 것이 느껴져 공부가 필요할 수도 있겠다는 생각이 들었다(미적분학 들어놓은 게 그나마 낳은 건가...)
출처
[1] Value Error, "딥러닝 활성화 함수 정리," *Tistory*, https://value-error.tistory.com/51 (accessed Feb. 4, 2025).
[2] Clay Ryu, "밑바닥부터 시작하는 딥러닝 (2): MNIST 신경망 구현," *Velog*, https://velog.io/@clayryu328/%EB%B0%91%EB%B0%94%EB%8B%A5%EB%B6%80%ED%84%B0-%EC%8B%9C%EC%9E%91%ED%95%98%EB%8A%94-%EB%94%A5%EB%9F%AC%EB%8B%9D-2-MNIST-%EC%8B%A0%EA%B2%BD%EB%A7%9D-%EA%B5%AC%ED%98%84 (accessed Feb. 4, 2025).
[3] Value Error, "MNIST 데이터셋을 이용한 신경망 구현," *Tistory*, https://value-error.tistory.com/54 (accessed Feb. 4, 2025).
[4] Twojun Space, "신경망 모델에서의 활성화 함수 이해하기," *Tistory*, https://twojun-space.tistory.com/124 (accessed Feb. 4, 2025).
-If any problem for references, or any questions please contact me by comments.
-This content is only for recording my studies and personal profiles
일부 출처는 사진 내에 표기되어 있습니다
본문의 내용은 학습과 개인 profile 이외의 다른 목적이 없습니다
출처 관련 문제 있을 시 말씀 부탁드립니다
상업적인 용도로 사용하는 것을 금합니다
본문의 내용을 Elixirr 강의자료 내용(권진욱 강사님)을 기반으로 제작되었습니다
깃허브 소스코드의 내용을 담고 있습니다
강의 커리큘럼이 '밑바닥부터 시작하는 딥러닝' 교재를 바탕으로 제작되었습니다
본문의 내용은 MS AI School 6기의 강의 자료 및 수업 내용을 담고 있습니다




